La palabra Trigonometría procede de las voces griegas tri-gonon-metron, que significa “medida de tres ángulos”. El objetivo prioritario de esta rama de las Matemáticas es el estudio de las medidas de los ángulos y lados de los triángulos. Las primeras aplicaciones de la trigonometría se hicieron en los campos de la navegación, la geodesia y la astronomía, en los que el principal problema era determinar una distancia inaccesible, es decir, una distancia que no podía ser medida de forma directa, como la distancia entre la Tierra y la Luna. Se encuentran notables aplicaciones de las funciones trigonométricas en la física y en casi todas las ramas de la ingeniería, sobre todo en el estudio de fenómenos periódicos y como se propagan las ondas: las ondas que se producen al tirar una piedra en el agua, o al agitar una cuerda cogida por los dos extremos, o las ondas electromagnéticas de la luz, el microondas o los rayos-x, las ondas sonoras, entre otros.
- Astronomía
Cálculo del radio de la Tierra, distancia de la Tierra a la Luna, distancia de la Tierra al Sol, predicción de eclipses, confección de calendarios, ... - Artillería
¿A qué distancia se encuentra un blanco al que se desea disparar con una catapulta o con un cañón? - Cartografía
Elaboración del mapa de un lugar del que se conocen algunas distancias y algunos ángulos. - Construcciones
Cómo construir un edificio para que cumpla ciertas exigencias de orientación. En qué dirección se excava un túnel para que salga, al otro lado de la montaña, en el lugar deseado. - Navegación
Construcción de cartas marinas en las que se detalle la ubicación de escollos, arrecifes, ...
Midiendo la altura de un edificio
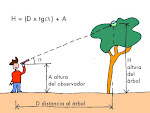
Para hallar la altura, H, de un edificio se miden la distancia desde el punto de observación a la base del edificio, D, y el ángulo θ (theta) que se muestra en el dibujo. El cociente entre la altura H y la distancia D es igual a la tangente de θ (H/D = tg θ). Para calcular H se multiplica la tangente de θ por la distancia D (H = Dtgθ). El ángulo se puede medir con exactitud utilizando un teodolito (instrumento destinado a ubicar un objeto a cierta distancia mediante la medida de ángulos con respecto al horizonte y con respecto a los puntos cardinales). Pero también se puede hacer uno con un transportador de ángulos, cilindro hueco (podria ser la parte que recubre un lapicero) y una plomada (hecha con algun peso que colgaremos de un hilo). Se sujeta la plomada en el origen del transportador; luego fijamos el cilindro a lo largo de la base del transportador y se apunta con la base de éste hacia el tejado del edificio. El ángulo buscado es 90º menos el formado por el hilo de la plomada.
Construye un teodolito casero como el que se mencionó anteriormente y prueba a medir ángulos de diversos objetos que observes.
Línea de visión
Se llama línea de visión a la recta imaginaria que une el ojo de un observador con el lugar observado. Llamamos ángulo de elevación al que forman la horizontal del observador y el lugar observado cuando éste está situado arriba del observador. Cuando el observador está más alto lo llamaremos ángulo de depresión.




hola bueno creo que sopy la primera o la unica en ver esta pagina je je bueno esto me ayudara ha hacer un proyecto de fisica GRACIAS a quien lo hizo atte: GoticaPaoLagrimaNegra
ResponderEliminarbueno bueno awan mas propa eeeee para k los vean mas me gusto interesante atto: m0n3kyta
ResponderEliminarMe sirvió muchísimo, gracias por compartir =)
ResponderEliminarSaludos desde Argentina.
Súper buena la información .... Gracias
ResponderEliminarmenuda mierda
ResponderEliminarMuchas gracias por la información brindada, me ha servido de gran ayuda para el estudio del tema y tareas.
ResponderEliminar